7.1 Definition

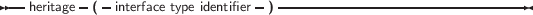
As of version 1.1, FPC supports interfaces. Interfaces are an alternative to multiple inheritance (where a class can have multiple parent classes) as implemented for instance in C++. An interface is basically a named set of methods and properties: a class that implements the interface provides all the methods as they are enumerated in the Interface definition. It is not possible for a class to implement only part of the interface: it is all or nothing.

Interfaces can also be ordered in a hierarchy, exactly as classes: an interface definition that inherits from another interface definition contains all the methods from the parent interface, as well as the methods explicitly named in the interface definition. A class implementing an interface must then implement all members of the interface as well as the methods of the parent interface(s).

An interface can be uniquely identified by a GUID. GUID is an acronym for Globally Unique Identifier, a 128-bit integer guaranteed always to be unique¹. Especially on Windows systems, the GUID of an interface can and must be used when using COM.

The definition of an Interface has the following form:

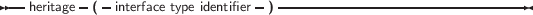
Along with this definition the following must be noted:

• Interfaces can only be used in DELPHI mode or in OBJFPC mode.
• There are no visibility specifiers. All members are public (indeed, it would make little sense to make them private or protected).
• The properties declared in an interface can only have methods as read and write specifiers.
• There are no constructors or destructors. Instances of interfaces cannot be created directly: instead, an instance of a class implementing the interface must be created.
• Only calling convention modifiers may be present in the definition of a method. Modifiers as virtual, abstract or dynamic, and hence also override cannot be present in the interface definition.

The following are examples of interfaces:

As can be seen, the GUID identifying the interface is optional.